Contents
はじめに:旅人算は「公式」で覚えると失敗する
「太郎くんが分速60m、次郎くんが分速40mで…」
算数のテキストでこの文章を見た瞬間、頭が痛くなるお子さん(あるいは大人の方)は多いものです。
旅人算が苦手になる最大の原因は、「出会いは足し算、追いかけっこは引き算」という公式を、意味もわからず丸暗記してしまうからです。
実は、旅人算の正体はシンプルです。
「2人の間の『距離』が、1分間にどれくらい縮まるか(あるいは広がるか)」。
これさえイメージできれば、複雑な公式は一切必要ありません。この記事では、図解イメージを使って旅人算を完全攻略します。
基本パターン1:「出会い算」は協力プレー
まずは、離れた場所にいる2人が、向かい合って進む「出会い」のパターンです。
【例題】
1000m離れた公園と駅から、太郎くん(分速60m)と次郎くん(分速40m)が同時に出発して向かい合って歩きます。2人が出会うのは何分後ですか?
考え方:2人で協力して距離を縮めている
この状況をイメージしてみましょう。
- 太郎くんが1分歩くと、距離は60m縮まります。
- 次郎くんが1分歩くと、距離は40m縮まります。
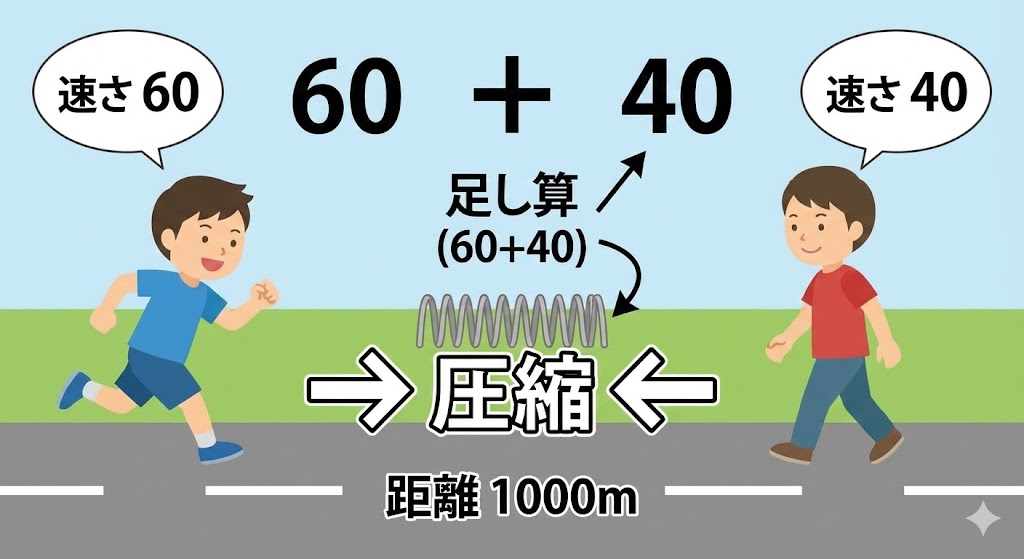
つまり、2人が同時に歩くと、1分間で「60m + 40m = 100m」ずつ距離が縮まっていくことになります。
1000mあった距離を、1分間に100mずつのペースで食べていく(縮めていく)わけですから、計算はこうなります。
1000m ÷ (60 + 40) = 10分後
これが「速さの和(足し算)」を使う理由です。2人が協力して距離を縮めているから、パワー(速さ)を合わせるのです。
基本パターン2:「追いかけ算」は逃走劇
次は、先行する相手を、足の速い人が後ろから追いかける「追いかけっこ」のパターンです。
【例題】
次郎くん(分速40m)が歩いて出発してから5分後に、太郎くん(分速60m)が追いかけます。
この時、2人の間には200mの差があります。太郎くんは何分で追いつきますか?
考え方:1分間にどれだけ差が詰まる?
ここが重要です。太郎くんが頑張って60m進んでも、その間に次郎くんも40m逃げてしまいます。
- 太郎くん「よし、60m近づいたぞ!」
- 次郎くん「へへーん、ボクも40m進んだよ」
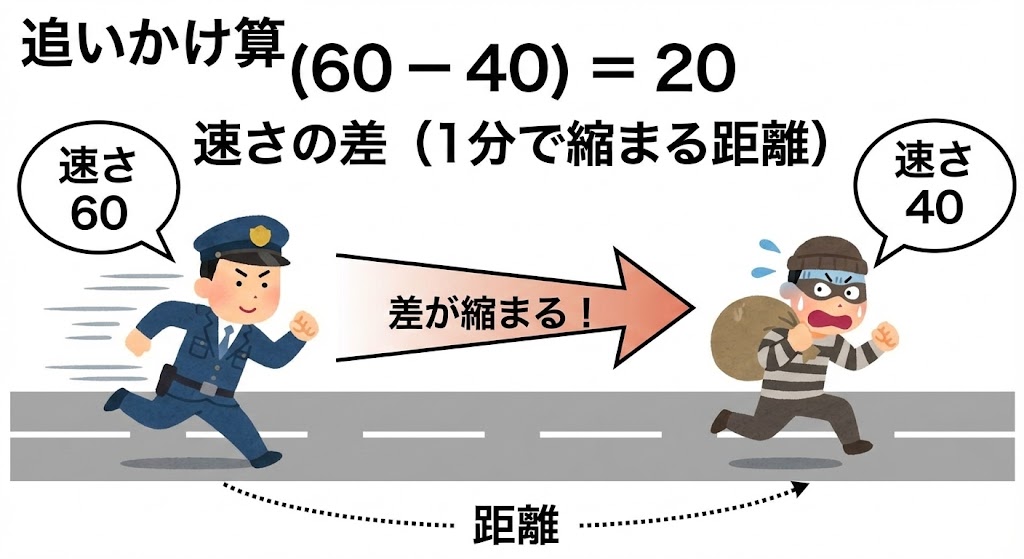
- 結果:「60m - 40m = 20m」しか差が縮まらない。
これが「追いかけ算」の本質です。
2人の能力の差(速さの差)だけが、毎分縮まっていきます。
200mある差を、1分間に20mずつのペースでじわじわ詰めていくわけですから、計算はこうなります。
200m ÷ (60 - 40) = 10分後
これが「速さの差(引き算)」を使う理由です。相手が逃げる分を差し引いたものが、実際に縮まる距離なのです。
絶対に間違えないための「線分図」の書き方
旅人算を解くとき、頭の中だけで計算しようとしてはいけません。必ず簡単な図(線分図)を描く癖をつけましょう。
- 一本の直線を引く: スタート地点とゴール(または相手のいる場所)を描きます。
- 矢印を描く: どちらに進んでいるか、矢印を描き込みます。向かい合っているなら「→ ←」、追いかけているなら「→ →」になります。
- 情報を書き込む: 「距離」「速さ」を書き込みます。
- 「1分後の世界」を想像する: 矢印の先に、「1分後に2人の距離はどうなったか?」を考えます。
この手順を踏めば、池の周りを回る問題や、往復する複雑な問題になっても、「結局、1分で何メートル縮まるの?」という基本に立ち返ることができます。
まとめ:旅人算は「2人の関係性」の物語
旅人算は、単なる数字の計算ではありません。
- 出会い算 = 協力して距離をゼロにする物語(足し算)
- 追いかけ算 = 逃げる相手との差を詰める物語(引き算)
このイメージさえ持てれば、もう公式を忘れても大丈夫。
「もし自分だったら?」と想像しながら、図を描いて解いてみてください。パズルを解くような面白さが見えてくるはずです。




